The Rule of 72 provides a straightforward method for calculating the time it takes for investments to double in value at a fixed annual interest rate. This practical formula serves as a mental shortcut that works better than complex financial calculators or spreadsheets.
The formula is straightforward: divide 72 by your expected rate of return to determine the number of years needed for your money to double. A dollar invested at a fixed 10% annual interest rate would take approximately 7.2 years to become $2. The calculation proves most accurate with interest rates from 5% to 10%, which covers many standard investment scenarios. This rule's versatility extends beyond investments and helps us understand how fast debt could double at a fixed rate. Such insights provide a valuable point of view on both investments and liabilities.
The Rule of 72 helps investors quickly grasp compound interest's impact. This fundamental financial concept deserves a closer look.
What is the Rule of 72 in finance?
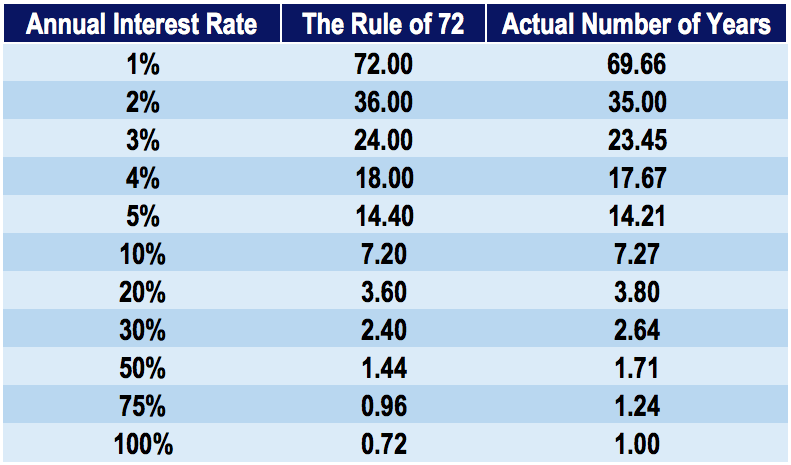
Image Source: Corporate Finance Institute
This mathematical shorthand estimates how long it will take for an investment to double in value at a specific annual return rate. The rule applies to compound interest calculations rather than simple interest.
You can flip this formula to find the interest rate needed to reach your financial goals. The calculation becomes simple - just divide 72 by your target doubling period in years. To name just one example, achieving a 6% annual return would double your investment in 12 years (72 ÷ 12 = 6).
These examples show how it works:
- At 1% return: 72 years to double
- At 2% return: 36 years to double
- At 7% return: 10 years to double
How it simplifies compound interest math
Complex logarithmic formulas are needed to calculate compound growth without the Rule of 72. The actual equation uses natural logarithms: t = 0.693147/r, where t represents time and r represents the rate.
The Rule of 72 turns this complex equation into a simple mental calculation. Financial experts call it a "back-of-the-envelope" method that yields accurate results. Scientific calculators and spreadsheet programs can compute exact figures, but this rule gives quick estimates when time matters.
Why 72 is used instead of 69.3
The number 69.3 (natural logarithm of 2 multiplied by 100) would be more mathematically precise for continuous compounding. Yet 72 proves more practical. Many convenient divisors make up the number 72 (1, 2, 3, 4, 6, 8, 9, and 12), which simplifies mental math.
Your situation might call for these adjustments to maximize accuracy:
- The Rule of 69.3 works best for continuous or daily compounding
- Think over using 71 instead of 72 for interest rates below 8%
- Add 1 to 72 for every 3 percentage points above 8%
All the same, the Rule of 72 gives enough accuracy for most financial planning needs while staying easy to remember and calculate.
How to Use the Rule of 72 in Everyday Scenarios
The Rule of 72 shows its real magic when you see how it works with your money. This simple formula helps you make smarter financial decisions every day.
How long does it take to double my money?
You can quickly see how different interest rates change your investment timeline with the Rule of 72. An investment earning 6% annually takes about 12 years to double (72 ÷ 6 = 12). Your money doubles in just 6 years with a 12% return.
Here's a quick look at doubling times:
- 3% return: 24 years to double
- 6% return: 12 years to double
- 12% return: 6 years to double
These numbers show why getting even a slightly better return rate makes a big difference over time. You can also flip the formula around - if you want to double your money in 6 years, you'll need about 12% annual returns (72 ÷ 6 = 12).
Using the rule for inflation and purchasing power
Inflation quietly eats away at your money's value. The Rule of 72 helps you figure out when inflation will cut your purchasing power in half.
Your money loses half its buying power in 24 years with 3% inflation. At 6% inflation, this drops to just 12 years. These numbers show why keeping cash at home means losing wealth as time passes.
Estimating the effect of investment fees
Small investment fees can really hurt your long-term growth. A tiny 1% fee changes how fast your money doubles.
Let's look at two funds with 7% returns but different fees: Fund A charges 0.5% (net return 6.5%) and doubles your money in 11.1 years. Fund B charges 1% (net return 6%) and takes 12 years. This gap grows huge over decades.
Debt growth and credit card interest
The Rule of 72 helps you understand debt growth too. Credit cards usually charge 18-30% interest. Your unpaid credit card balance doubles in just 3.6 years at 20% interest if you only make minimum payments.
The situation gets worse at 24% interest - your debt doubles in only 3 years. This explains how credit card debt can quickly get out of hand. You can avoid this trap by using strategies like the debt avalanche method - paying off your highest-interest debts first.
Want to check your own financial timeline? Try a Rule of 72 calculator to see how quickly your money doubles at different interest rates or how fast your debt might grow if you don't pay it off.
Comparing the Rule of 72 with Other Methods
Mathematical shortcuts beyond the Rule of 72 help estimate investment doubling time. You need to understand how these methods are different to pick the right one that fits your needs.
Rule of 72 vs. Rule of 69.3 vs. Rule of 70
These three rules serve the same purpose but each one works better in specific cases. The Rule of 72 gives the best results with annual compounding at common interest rates (6% to 10%). It also divides easily by many numbers (1, 2, 3, 4, 6, 8, 9, and 12). The Rule of 69.3 matches the actual natural logarithm value and works better for continuous or daily compounding. The Rule of 70 gives good estimates for growth rates under 10%, which makes it useful for economic calculations like GDP growth.
Here's how they compare:
| Rule | Best For | Example (8% interest) |
|---|---|---|
| 72 | Annual compounding, rates 6-10% | 9 years |
| 69.3 | Continuous compounding, all rates | 8.66 years |
| 70 | Economic calculations, lower rates | 8.75 years |
When to use each rule
The Rule of 72 works best with interest rates between 6% and 10% that compound annually. You can adjust it by adding or subtracting 1 from 72 for every 3 points the interest rate is different from 8%. The Rule of 69.3 (or rounded to 69 or 70) fits daily or continuous compounding situations better. The Rule of 70 shines in economic scenarios with modest growth rates.
Using logarithms for exact results
The logarithmic formula T = ln(2)/ln(1+(r/100)) calculates the exact doubling time. Take an 8% annual return as an example - the exact calculation shows 9.006 years, which matches the Rule of 72's estimate of 9 years almost perfectly. These rules are great for quick estimates, but logarithmic calculations give you the most accurate results.
Tips for Smarter Financial Planning with the Rule
Image Source: Hudson Financial Planning
The rule of 72 becomes more powerful when you apply these practical tips to your financial planning.
Using a Rule of 72 calculator
Rule of 72 calculators available online give you quick estimates and exact answers from compound interest calculations. You can compare different investments and see their growth potential with these tools. Why not check how long it takes for your money to double using different interest rates? Many investors feel motivated to extend their investment timeline after this simple exercise.
Adjusting the rule for better accuracy
Your specific situation determines the best way to adjust this rule. The rule of 69.3 for continuous compounding works better in some cases. Interest rates below 8% work better with 71 instead of 72. The calculation needs an extra point added to 72 for every 3 percentage points above 8%. These adjustments give you more accurate estimates in different scenarios.
Incorporating the rule into retirement planning
The rule of 72 proves invaluable in retirement planning. Your $250,000 needs to double twice to reach $1 million for retirement. An 8% return would take about 18 years total. This calculation shows if your strategy needs adjustments or if you're on the right path.
Avoiding common mistakes with the formula
Several mistakes can throw off your calculations. Always use APY instead of APR. Remember to subtract fees from expected returns. Use inflation-adjusted returns in your calculations. Market returns fluctuate naturally - don't expect consistency. The formula works best for long-term planning rather than short-term goals.
Conclusion
The Rule of 72 helps turn complex financial math into simple mental calculations. This piece shows how this elegant formula lets us estimate investment doubling time, understand how inflation affects our money, and see the real cost of debt quickly. The rule works in daily financial decisions without needing advanced math skills.
Success with money depends on understanding compound growth. Learning this rule gives you a vital edge when you plan retirement, look at investment chances, or choose between financial products with different fees. A 3% return takes 24 years to double your money while a 12% return takes just 6 years. This shows why finding better returns matters so much over time.
The Rule of 72 gives great estimates, but note that it has limits. You get the best results with interest rates between 5-10% and yearly compounding. The Rule of 69.3 or Rule of 70 might work better outside these ranges. Logarithmic calculations remain the best choice when you need perfect accuracy.
This simple formula helps you gage potential outcomes fast when making money decisions. The Rule of 72 gives you quick insights to make smarter choices about investments, debt growth, or retirement planning. Money skills start with practical tools we can use daily. This rule stands out as one of the most useful concepts in personal finance.
Key Takeaways
The Rule of 72 is a simple yet powerful financial tool that helps you quickly estimate investment growth and make smarter money decisions without complex calculations.
• Divide 72 by your interest rate to find doubling time - At 8% return, your money doubles in 9 years (72 ÷ 8 = 9)
• Small rate differences create massive long-term impact - 6% return doubles money in 12 years, while 12% return does it in just 6 years
• Use it to understand inflation's hidden cost - At 3% inflation, your purchasing power halves every 24 years
• Apply the rule to debt management - Credit card debt at 20% interest doubles in just 3.6 years if unpaid
• Works best for rates between 5-10% with annual compounding - For other scenarios, consider Rule of 69.3 or precise logarithmic calculations
This mental shortcut transforms intimidating compound interest math into quick estimates that guide retirement planning, investment comparisons, and debt strategies. Whether you're evaluating investment opportunities or understanding how fees impact long-term growth, the Rule of 72 provides immediate insights for better financial decision-making.
FAQs
Q1. How does the Rule of 72 work for calculating investment growth? The Rule of 72 is a simple formula where you divide 72 by the annual rate of return to estimate how many years it will take for an investment to double. For example, with an 8% annual return, it would take approximately 9 years for your investment to double (72 ÷ 8 = 9).
Q2. Can the Rule of 72 be applied to understand the impact of inflation? Yes, the Rule of 72 can be used to estimate how quickly inflation erodes purchasing power. For instance, with 3% annual inflation, your money's purchasing power would halve in about 24 years (72 ÷ 3 = 24).
Q3. Is the Rule of 72 accurate for all interest rates? The Rule of 72 works best for interest rates between 5% and 10% with annual compounding. For rates outside this range or for continuous compounding, other methods like the Rule of 69.3 or precise logarithmic calculations may be more accurate.
Q4. How can the Rule of 72 help in retirement planning? The Rule of 72 can quickly show how long it might take to reach your retirement goals. For example, if you need your investments to double twice to reach your target, and you expect an 8% annual return, it would take approximately 18 years (9 years to double, then another 9 years to double again).
Q5. Can the Rule of 72 be used to understand debt growth? Absolutely. The Rule of 72 can illustrate how quickly debt can grow, especially with high-interest rates. For instance, credit card debt with a 24% annual interest rate would double in just 3 years if left unpaid (72 ÷ 24 = 3), highlighting the importance of paying off high-interest debt quickly.
